
How much can a human body be scaled before the physics break down? This was the question a VFX artist asked me last night at the New Orleans VFX & 3D Animation Meetup.
A quick answer comes from looking at the tallest and shortest people that have ever survived into adulthood. The world’s shortest living person is about two feet tall, while the tallest person is over 8 feet. This gives us the range of sizes at which human beings can actually live.
However, we can’t overlook the fact that very tall and small people tend to have health issues related to their sizes. Robert Wadlow, the tallest living man in the world in 1940, never stopped growing. By the time he reached 8’11” at the age of 22, his body’s systems had deteriorated so much that he died from a simple infection.
On the shorter side, persons with dwarfism will often have some normal-sized body parts, leading to the need for surgery to live normally. For example, a set of adult-sized tonsils in a child-sized neck might block breathing to the point where the body can’t get enough oxygen.
These difficulties point to the idea that scaling the human body too much beyond a normal range will lead to problems with internal functions.
VFX People and Volume
But enough about real people. What about extremely large or small people who live only in the world of fantasy, like the Incredible Hulk and the Brownies in the film Willow? To get an idea of whether such people could live at all, we need to look at the way the different systems in the body are affected by a change in scale.
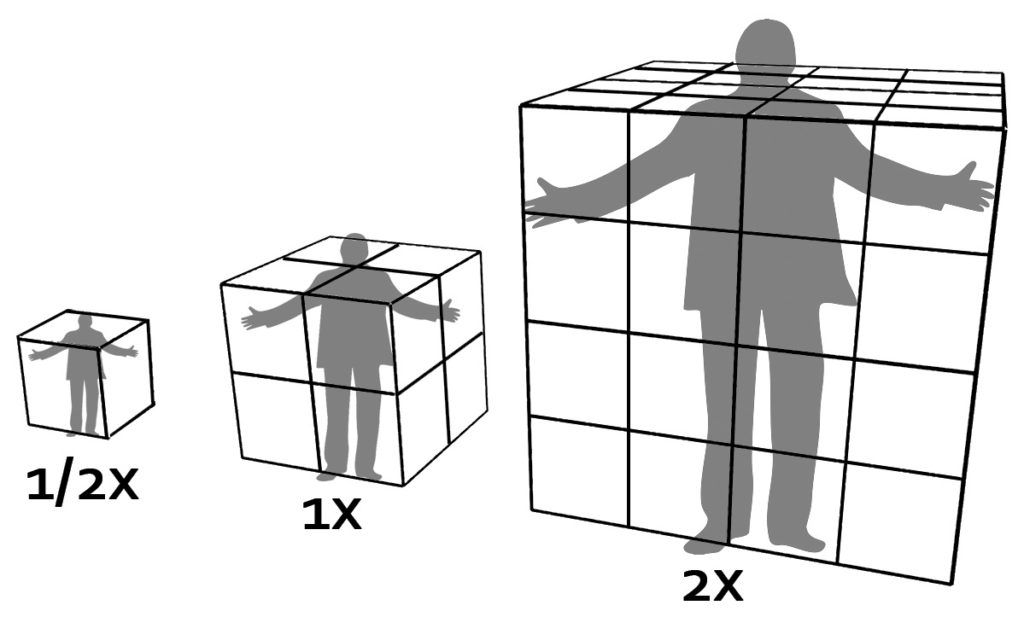
Human beings are three-dimensional creatures; they have a height, width and depth. To approximate a body’s volume, you can work with cubes to get a rough idea. The volume of a cube is height x width x depth. We use this concept of cube volumes to help us understand what happens when a human body is scaled.
If you scale a person, it’s not just his height that changes; it’s his width and depth too. If a body is scaled in such a way that the height is increased by a factor of 2 (twice as tall), the body volume increases by a factor of 8, which is 2 cubed. Volume is directly related to weight, so a 2x body will weigh 8 times more than the original.
Big People, Big Muscles
Muscles don’t change in scale the same way volume does. The strength of a muscle is related to its width x depth, and has little to do with its height. For this reason, muscle strength in a 2x body would increase by only 4x. In the original body, the leg muscles were big enough (and thus strong enough) to lift the weight of the leg so the person could walk, run, and jump. But in a 2x body, those 4x muscles would struggle to lift those 8x heavier legs.
One solution is to make the muscles very large in proportion to the overall size of the body. Then the musclebound character could, presumably, lift those legs with ease. We often see this approach in comic book characters and superheros.

Tiny People, Fast Hearts
Conversely, a half-height person would have 1/8 the weight and volume of a normal-sized person, but muscle strength would decrease to only 1/4. Like an ant, the tiny human would have the strength to lift far more than its own body weight.
But this reduced size comes with a price. Organs like the heart and lungs reduce in volume, too. With a 1/8 sized heart, the amount of blood being pumped to these 1/4 muscles is half of what they’re accustomed to. To get enough blood to its muscles, a tiny human’s heart would have to beat twice as fast. With the 1/8 sized lungs, the tiny human would have to breathe twice as fast to get enough oxygen into its blood.
Fast heartbeats and breathing rates are associated with fast, scampering movements (think mice and squirrels). A tinier voicebox also means a more high-pitched voice.
So far, we’re on target for describing the Brownies from Willow, but the physics falls down on lifespan. Animals with fast heart rates only live a few years. Brownies, on the other hand, are said to live for 1000 years.
The physics of human scale is covered in detail in Chapter 5 of Physics for Animators.
